양말이 뒤섞인 양말 뭉치에서 2개의 양말을 임의로 꺼내면, 대부분 짝짝이 양말이 나온다. 왜 그럴까? 수학의 조합 원리를 이용하면, 이런 상황의 확률 값을 구해 확인할 수 있다.
먼저 간단한 상황에서 확률 값을 구해 보자. 서랍 속에 완벽하게 짝이 맞는 6짝(3종류)의 양말이 있다. 양말은 마구 뒤섞여 있고, 이 양말 뭉치에서 2개의 양말을 꺼낸다고 가정해 보자. 짝짝이 양말을 뽑을 확률은 얼마일까?
먼저 6개의 양말에서 2개의 양말을 임의로 뽑는 경우의 수는 조합공식에 의해 6!÷(2!×4!) = 15가지다. 이 값이 전체 경우의 수가 된다. 이제 6개의 양말 중에서 2개를 뽑을 때, 그 2개가 서로 다른 양말일 경우를 생각해 보자.
3종류의 양말 중에서 서로 다른 2종류의 양말을 선택할 경우는 3가지다. 그런데 이 3가지에서 각각의 종류마다 양말이 2짝씩 있다. 예를 들어 A모양 양말과 B모양 양말을 뽑았을 때, 서랍 속에는 A모양 양말 2개, B모양 양말이 2개 있어 짝짝이 양말을 뽑는 경우의 수는 2×2=4(가지)가 된다. 그러므로 6개의 양말 중에서 2개를 뽑았을 때, 그 양말이 모두 짝짝이일 경우의 수는 4+4+4=12가지다.
전체 경우의 수는 15가지이므로, 6개의 양말 중에서 2개를 뽑았을 때 짝짝이 양말을 뽑을 확률은 12÷15로 80%다. 즉, 임의로 양말 2짝을 뽑았을 때 짝짝이가 나오는 것은 확률적으로 가능성이 큰 사건임을 알 수 있다.
게다가 여기서 구한 80%란 확률 값은 양말이 6개, 고작 3켤레인 경우의 값이다. 양말의 개수를 10개로 늘이면 확률 값은 약 88.89%, 양말의 개수를 20개로 늘이면 무려 94.74%로 커진다. 짝짝이 양말을 뽑은 게 불운이 아니라 짝짝이를 뽑지 않은 것이 행운임에 분명하다.
양말 뭉치에서 짝짝이를 선택할 확률을 구하는 공식을 만들 수 있다. n개의 양말 뭉치에서 2s개를 임의로 뽑았을 때, 나머지 양말 중에서 짝을 이루고 있는 것이 2d일 확률 P의 값은 다음과 같다.
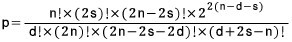
'교육 > 별별지식' 카테고리의 다른 글
| 여성인권과 일본 여고생 체육복 부르마 이야기 (0) | 2014.12.21 |
|---|---|
| 패러독스 (역설) - 모순 (0) | 2014.12.10 |
| 경찰 마스코트 포돌이에게 6가지 의미가 있다? (0) | 2014.12.07 |
| 내가 서는 줄만 다른 줄에 비해 줄지 않는 이유 (0) | 2014.12.01 |
| 쨈 바른 토스트는 왜 맨날 쨈을 발라 놓은 쪽이 떨어질까? (0) | 2014.12.01 |
| 모나미 153 볼펜 이름 유래 (0) | 2014.11.28 |
| 칠성사이다는 왜 이름이 칠성일까? (0) | 2014.11.28 |
| 빨간색 스포츠카가 더 시끄럽다고? (0) | 2014.05.30 |





댓글