'더하기' 태그의 글 목록
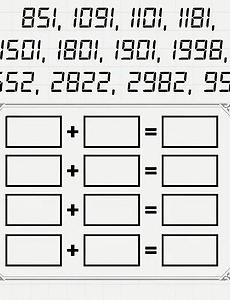제시된 모든 수를 사용해 네 개의 식을 만들어야 하는 산수 문제
851, 1091, 1101, 1181, 1501, 1801, 1901, 1998, 2652, 2822, 2982, 9512모두 12개의 수가 있다. 이 수를 모두 사용해서 네 개의 식을 만들어야 한다. 아래 각각의 빈 칸에 위에 나열된 수를 모두 넣어서 제대로 된 식으로 완성해야 하는 것이 오늘의 문제, 시간과의 싸움이기도 하지만 창조적인 아이디어도 필요한 고난도 문제다.하나의 식은 완성할 수 있어도 다음 수식까지 완성하려면 수를 활용해야 하는 능력이 뛰어나야 한다. 풀이가 너무 어려워서 시작조차 못 하는 분도 있겠지만 언제나 답은 있는 법, 아래 패널들의 잡담이 무의미해도 답이라는 건 엉뚱한 장소와 예상하지 못하는 곳에서 출몰하는 법, 잡담이 하나의 힌트가 될 수 있다생각외로 너무 어려워서 중간에 토..
2017. 11. 6.
알록달록 의상으로 푸는 덧셈 뺄셈 사칙연산 산수 문제
아래 그림이 준비되어 있다. 그림에는 다양한 의상이 있는데 티셔츠, 양말, 반바지, 청바지, 속옷, 치마, 모자, 원피스, 하이힐 등 다양하게 구비되어 있다. 다음 의상들의 수식에서 답으로 와야 하는 의상이 무엇인지 알아내야 하는 문제알록달록한 의상에 몹시 당황스럽겠지만 생각보다 아주 쉬운(!) 문제다. 그림을 어떻게 변환해야 하는지만 알면 더하기, 빼기 문제이기 때문에 답 찾기는 수월하다. 아마도 대부분 그림에 나온 의상들의 여러가지 색상을 보고 영단어 혹은 글자 수로 해석하려고 할텐데 애초에 그런 식의 접근이었다면 문제로 나오지도 않았다, 무엇보다 색깔로 바꾼다해도 그걸 어떻게 더하고 뺄지는 역시 해결 포인트가 아니기 때문에 다른 식의 접근이 필요하다, 더군다나 문제가 되는 스커트 더하기 원피스 빼기..
2017. 11. 3.
원래 정답 보다 이용진의 오답 풀이가 더 와닿는 알파벳 더하기 문제
문제적 남자에서 이용진이 오답으로 가장 먼저 풀었던 문제, 하지만 본래의 정답 보다 오히려 이용진의 오답 풀이와 오답이 더 문제 같았던 문제다. 정답의 경우에는 되려 약간 애매한 구석이 있다. 알파벳을 더하면 특정 셈이 성립되는데 숨겨진 규칙을 맞혀야 한다. 알파벳 더하기 문제, 주어진 문제는 다음과 같다.N + Q = 11H + B = 14L + T = ?이용진의 답 풀이알파벳 획과 더하기, 등호, 거기에 정답 숫자까지 모두 획을 더하면 모양이 갖추어진다. N은 획이 3번, 더하기는 획이 2번, Q도 획이 2번 등호(이콜)도 2번, 숫자 11도 2번, 모두 더하면 답 11, H + B = 14 도 마찬가지다. 신기하게 획과 수식이 모두 같은 상황, 이게 맞다면 대박이고 틀리더라도 대박이다.정작 멋지게 ..
2016. 6. 30.
